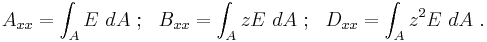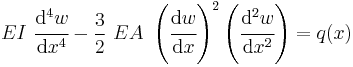Euler–Bernoulli beam equation
| Continuum mechanics |
|---|
Euler–Bernoulli beam theory (also known as engineer's beam theory, classical beam theory or just beam theory)[1] is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only. It is thus a special case of Timoshenko beam theory which accounts for shear deformation and is applicable for thick beams. It was first enunciated circa 1750,[2] but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
Additional analysis tools have been developed such as plate theory and finite element analysis, but the simplicity of beam theory makes it an important tool in the sciences, especially structural and mechanical engineering.
Contents |
History
Prevailing consensus is that Galileo Galilei made the first attempts at developing a theory of beams, but recent studies argue that Leonardo da Vinci was the first to make the crucial observations. Da Vinci lacked Hooke's law and calculus to complete the theory, whereas Galileo was held back by an incorrect assumption he made.[3]
The Bernoulli beam is named after Jacob Bernoulli, who made the significant discoveries. Leonhard Euler and Daniel Bernoulli were the first to put together a useful theory circa 1750.[4] At the time, science and engineering were generally seen as very distinct fields, and there was considerable doubt that a mathematical product of academia could be trusted for practical safety applications. Bridges and buildings continued to be designed by precedent until the late 19th century, when the Eiffel Tower and Ferris wheel demonstrated the validity of the theory on large scales.
For practical purposes, such as in the European design codes, it has now been superseded by the Perry Robertson formula which takes account of initial deflection of the beam.[5]
Static beam equation
The Euler-Bernoulli equation describes the relationship between the beam's deflection and the applied load[6]:
The curve  describes the deflection
describes the deflection  of the beam at some position
of the beam at some position  (recall that the beam is modeled as a one-dimensional object).
(recall that the beam is modeled as a one-dimensional object).  is a distributed load, in other words a force per unit length (analogous to pressure being a force per area); it may be a function of
is a distributed load, in other words a force per unit length (analogous to pressure being a force per area); it may be a function of  ,
,  , or other variables.
, or other variables.
Note that  is the elastic modulus and that
is the elastic modulus and that  is the second moment of area.
is the second moment of area.  must be calculated with respect to the centroidal axis perpendicular to the applied loading. For an Euler-Bernoulli beam not under any axial loading this axis is called the neutral axis.
must be calculated with respect to the centroidal axis perpendicular to the applied loading. For an Euler-Bernoulli beam not under any axial loading this axis is called the neutral axis.
Often,  ,
, 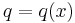 , and EI is a constant, so that:
, and EI is a constant, so that:
This equation, describing the deflection of a uniform, static beam, is used widely in engineering practice. Tabulated expressions for the deflection  for common beam configurations can be found in engineering handbooks. For more complicated situations the deflection can be determined by solving the Euler-Bernoulli equation using techniques such as the "slope deflection method", "moment distribution method", "moment area method, "conjugate beam method", "the principle of virtual work", "direct integration", "Castigliano's method", "Macaulay's method" or the "direct stiffness method".
for common beam configurations can be found in engineering handbooks. For more complicated situations the deflection can be determined by solving the Euler-Bernoulli equation using techniques such as the "slope deflection method", "moment distribution method", "moment area method, "conjugate beam method", "the principle of virtual work", "direct integration", "Castigliano's method", "Macaulay's method" or the "direct stiffness method".
Successive derivatives of  have important meanings:
have important meanings:
-
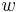 is the deflection.
is the deflection.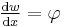 is the slope of the beam.
is the slope of the beam.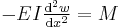 is the bending moment in the beam.
is the bending moment in the beam.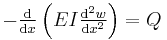 is the shear force in the beam.
is the shear force in the beam.
The stresses in a beam can be calculated from the above expressions after the deflection due to a given load has been determined.
A number of different sign conventions can be found in the literature on the bending of beams and care should be taken to maintain consistency.[6] In this article, the sign convention has been chosen so the coordinate system is right handed. Forces acting in the positive  and
and 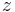 directions are assumed positive. The sign of the bending moment is chosen so that a positive value leads to a tensile stress at the bottom cords. The sign of the shear force has been chosen such that it matches the sign of the bending moment.
directions are assumed positive. The sign of the bending moment is chosen so that a positive value leads to a tensile stress at the bottom cords. The sign of the shear force has been chosen such that it matches the sign of the bending moment.
Dynamic beam equation
The dynamic beam equation is the Euler-Lagrange equation for the following action
The first term represents the kinetic energy where  is the mass per unit length; the second one represents the potential energy due to internal forces (when considered with a negative sign) and the third term represents the potential energy due to the external load
is the mass per unit length; the second one represents the potential energy due to internal forces (when considered with a negative sign) and the third term represents the potential energy due to the external load 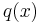 . The Euler-Lagrange equation is used to determine the function that minimizes the functional
. The Euler-Lagrange equation is used to determine the function that minimizes the functional  . For a dynamic Euler-Bernoulli beam, the Euler-Lagrange equation is
. For a dynamic Euler-Bernoulli beam, the Euler-Lagrange equation is
-
Derivation of Euler–Lagrange equation for beams Since the Lagrangian is the corresponding Euler-Lagrange equation is
Now,
Plugging into the Euler-Lagrange equation gives
or,
which is the governing equation for the dynamics of an Euler-Bernoulli beam.
Stress
Besides deflection, the beam equation describes forces and moments and can thus be used to describe stresses. For this reason, the Euler–Bernoulli beam equation is widely used in engineering, especially civil and mechanical, to determine the strength (as well as deflection) of beams under bending.
Both the bending moment and the shear force cause stresses in the beam. The stress due to shear force is maximum along the neutral axis of the beam (when the width of the beam, t, is constant along the cross section of the beam; otherwise an integral involving the first moment and the beam's width needs to be evaluated for the particular cross section), and the maximum tensile stress is at either the top or bottom surfaces. Thus the maximum principal stress in the beam may be neither at the surface nor at the center but in some general area. However, shear force stresses are negligible in comparison to bending moment stresses in all but the stockiest of beams as well as the fact that stress concentrations commonly occur at surfaces, meaning that the maximum stress in a beam is likely to be at the surface.
Simple or symmetrical bending
For beam cross-sections that are symmetrical about a plane perpendicular to the neutral plane, it can be shown that the tensile stress experienced by the beam may be expressed as:
Here, 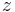 is the distance from the neutral axis to a point of interest; and
is the distance from the neutral axis to a point of interest; and  is the bending moment. Note that this equation implies that pure bending (of positive sign) will cause zero stress at the neutral axis, positive (tensile) stress at the "top" of the beam, and negative (compressive) stress at the bottom of the beam; and also implies that the maximum stress will be at the top surface and the minimum at the bottom. This bending stress may be superimposed with axially applied stresses, which will cause a shift in the neutral (zero stress) axis.
is the bending moment. Note that this equation implies that pure bending (of positive sign) will cause zero stress at the neutral axis, positive (tensile) stress at the "top" of the beam, and negative (compressive) stress at the bottom of the beam; and also implies that the maximum stress will be at the top surface and the minimum at the bottom. This bending stress may be superimposed with axially applied stresses, which will cause a shift in the neutral (zero stress) axis.
Maximum stresses at a cross-section
The maximum tensile stress at a cross-section is at the location 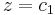 and the maximum compressive stress is at the location
and the maximum compressive stress is at the location 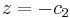 where the height of the cross-section is
where the height of the cross-section is 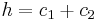 . These stresses are
. These stresses are
The quantities 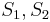 are the section moduli[6] and are defined as
are the section moduli[6] and are defined as
The section modulus combines all the important geometric information about a beam's section into one quantity. For the case where a beam is doubly symmetric, 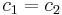 and we have one section modulus
and we have one section modulus 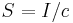 .
.
Strain in an Euler–Bernoulli beam
We need an expression for the strain in terms of the deflection of the neutral surface to relate the stresses in an Euler-Bernoulli beam to the deflection. To obtain that expression we use the assumption that normals to the neutral surface remain normal during the deformation and that deflections are small. These assumptions imply that the beam bends into an arc of a circle of radius  (see Figure 1) and that the neutral surface does not change in length during the deformation.[6]
(see Figure 1) and that the neutral surface does not change in length during the deformation.[6]
Let 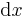 be the length of an element of the neutral surface in the undeformed state. For small deflections, the element does not change its length after bending but deforms into an arc of a circle of radius
be the length of an element of the neutral surface in the undeformed state. For small deflections, the element does not change its length after bending but deforms into an arc of a circle of radius  . If
. If 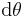 is the angle subtended by this arc, then
is the angle subtended by this arc, then 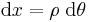 .
.
Let us now consider another segment of the element at a distance 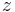 above the neutral surface. The initial length of this element is
above the neutral surface. The initial length of this element is 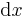 . However, after bending, the length of the element becomes
. However, after bending, the length of the element becomes 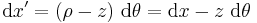 . The strain in that segment of the beam is given by
. The strain in that segment of the beam is given by
where  is the curvature of the beam. This gives us the axial strain in the beam as a function of distance from the neutral surface. However, we still need to find a relation between the radius of curvature and the beam deflection
is the curvature of the beam. This gives us the axial strain in the beam as a function of distance from the neutral surface. However, we still need to find a relation between the radius of curvature and the beam deflection  .
.
Relation between curvature and beam deflection
Let P be a point on the neutral surface of the beam at a distance  from the origin of the
from the origin of the 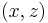 coordinate system. The slope of the beam, i.e., the angle made by the neutral surface with the
coordinate system. The slope of the beam, i.e., the angle made by the neutral surface with the  -axis, at this point is
-axis, at this point is
Therefore, for an infinitesimal element 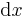 , the relation
, the relation 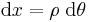 can be written as
can be written as
Hence the strain in the beam may be expressed as
Stress-strain relations
For a one-dimensional linear elastic material, the stress is related to the strain by 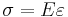 where
where  is the Young's modulus. Hence the stress in an Euler-Bernoulli beam is given by
is the Young's modulus. Hence the stress in an Euler-Bernoulli beam is given by
Note that the above relation, when compared with the relation between the axial stress and the bending moment, leads to
Since the shear force is given by 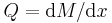 , we also have
, we also have
Boundary considerations
The beam equation contains a fourth-order derivative in  . To find a unique solution
. To find a unique solution 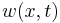 we need four boundary conditions. The boundary conditions usually model supports, but they can also model point loads, distributed loads and moments. The support or displacement boundary conditions are used to fix values of displacement (
we need four boundary conditions. The boundary conditions usually model supports, but they can also model point loads, distributed loads and moments. The support or displacement boundary conditions are used to fix values of displacement ( ) and rotations (
) and rotations (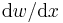 ) on the boundary. Such boundary conditions are also called Dirichlet boundary conditions. Load and moment boundary conditions involve higher derivatives of
) on the boundary. Such boundary conditions are also called Dirichlet boundary conditions. Load and moment boundary conditions involve higher derivatives of  and represent momentum flux. Flux boundary conditions are also called Neumann boundary conditions.
and represent momentum flux. Flux boundary conditions are also called Neumann boundary conditions.
As an example consider a cantilever beam that is built-in at one end and free at the other as shown in the adjacent figure. At the built-in end of the beam there cannot be any displacement or rotation of the beam. This means that at the left end both deflection and slope are zero. Since no external bending moment is applied at the free end of the beam, the bending moment at that location is zero. In addition, if there is no external force applied to the beam, the shear force at the free end is also zero.
Taking the  coordinate of the left end as
coordinate of the left end as  and the right end as
and the right end as  (the length of the beam), these statements translate to the following set of boundary conditions (assume
(the length of the beam), these statements translate to the following set of boundary conditions (assume 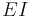 is a constant):
is a constant):
A simple support (pin or roller) is equivalent to a point force on the beam which is adjusted in such a way as to fix the position of the beam at that point. A fixed support or clamp, is equivalent to the combination of a point force and a point torque which is adjusted in such a way as to fix both the position and slope of the beam at that point. Point forces and torques, whether from supports or directly applied, will divide a beam into a set of segments, between which the beam equation will yield a continuous solution, given four boundary conditions, two at each end of the segment. Assuming that the product EI is a constant, and defining 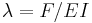 where F is the magnitude of a point force, and
where F is the magnitude of a point force, and 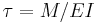 where M is the magnitude of a point torque, the boundary conditions appropriate for some common cases is given in the table below. The change in a particular derivative of w across the boundary as x increases is denoted by
where M is the magnitude of a point torque, the boundary conditions appropriate for some common cases is given in the table below. The change in a particular derivative of w across the boundary as x increases is denoted by  followed by that derivative. For example,
followed by that derivative. For example, 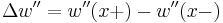 where
where 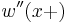 is the value of
is the value of 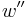 at the lower boundary of the upper segment, while
at the lower boundary of the upper segment, while 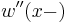 is the value of
is the value of 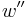 at the upper boundary of the lower segment. When the values of the particular derivative are not only continuous across the boundary, but fixed as well, the boundary condition is written e.g.
at the upper boundary of the lower segment. When the values of the particular derivative are not only continuous across the boundary, but fixed as well, the boundary condition is written e.g. 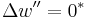 which actually constitutes two separate equations (e.g.
which actually constitutes two separate equations (e.g.  = fixed).
= fixed).
-
Boundary 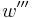
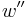
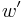

Clamp 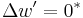
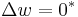
Simple support 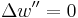
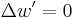
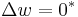
Point force 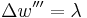
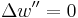
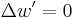
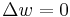
Point torque 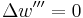
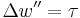
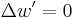
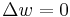
Free end 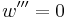
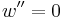
Clamp at end 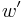 fixed
fixed fixed
fixedSimply supported end 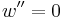
 fixed
fixedPoint force at end 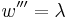
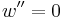
Point torque at end 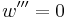
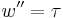
Note that in the first cases, in which the point forces and torques are located between two segments, there are four boundary conditions, two for the lower segment, and two for the upper. When forces and torques are applied to an end of the beam, there are two boundary conditions given which apply at that end.
Loading considerations
Applied loads may be represented either through boundary conditions or through the function 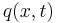 which represents an external distributed load. Using distributed loading is often favorable for simplicity. Boundary conditions are, however, often used to model loads depending on context; this practice being especially common in vibration analysis.
which represents an external distributed load. Using distributed loading is often favorable for simplicity. Boundary conditions are, however, often used to model loads depending on context; this practice being especially common in vibration analysis.
By nature, the distributed load is very often represented in a piecewise manner, since in practice a load isn't typically a continuous function. Point loads can be modeled with help of the Dirac delta function. For example, consider a static uniform cantilever beam of length  with an upward point load
with an upward point load  applied at the free end. Using boundary conditions, this may be modeled in two ways. In the first approach, the applied point load is approximated by a shear force applied at the free end. In that case the governing equation and boundary conditions are:
applied at the free end. Using boundary conditions, this may be modeled in two ways. In the first approach, the applied point load is approximated by a shear force applied at the free end. In that case the governing equation and boundary conditions are:
Alternatively we can represent the point load as a distribution using the Dirac function. In that case the equation and boundary conditions are
Note that shear force boundary condition (third derivative) is removed, otherwise there would be a contradiction. These are equivalent boundary value problems, and both yield the solution
The application of several point loads at different locations will lead to 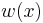 being a piecewise function. Use of the Dirac function greatly simplifies such situations; otherwise the beam would have to be divided into sections, each with four boundary conditions solved separately. A well organized family of functions called Singularity functions are often used as a shorthand for the Dirac function, its derivative, and its antiderivatives.
being a piecewise function. Use of the Dirac function greatly simplifies such situations; otherwise the beam would have to be divided into sections, each with four boundary conditions solved separately. A well organized family of functions called Singularity functions are often used as a shorthand for the Dirac function, its derivative, and its antiderivatives.
Dynamic phenomena can also be modeled using the static beam equation by choosing appropriate forms of the load distribution. As an example, the free vibration of a beam can be accounted for by using the load function:
where  is the linear mass density of the beam, not necessarily a constant. With this time-dependent loading, the beam equation will be a partial differential equation:
is the linear mass density of the beam, not necessarily a constant. With this time-dependent loading, the beam equation will be a partial differential equation:
Another interesting example describes the deflection of a beam rotating with a constant angular frequency of  :
:
This is a centripetal force distribution. Note that in this case,  is a function of the displacement (the dependent variable), and the beam equation will be an autonomous ordinary differential equation.
is a function of the displacement (the dependent variable), and the beam equation will be an autonomous ordinary differential equation.
Examples
Three-point bending
The three point bending test is a classical experiment in mechanics. It represents the case of a beam resting on two roller supports and subjected to a concentrated load applied in the middle of the beam. The shear is constant in absolute value: it is half the central load, P / 2. It changes sign in the middle of the beam. The bending moment varies linearly from one end, where it is 0, and the center where its absolute value is PL / 4, is where the risk of rupture is the most important. The deformation of the beam is described by a polynomial of third degree over a half beam (the other half being symmetrical). The bending moments ( ) , shear forces (
) , shear forces ( ), and deflections (
), and deflections ( ) for a beam subjected to a central point load and an asymmetric point load are given in the table below.[6]
) for a beam subjected to a central point load and an asymmetric point load are given in the table below.[6]
| Distribution | Max. value | |
|---|---|---|
| Simply supported beam with central load | ||
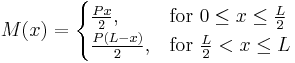 |
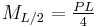 |
|
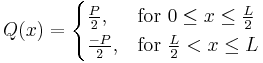 |
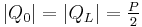 |
|
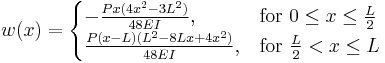 |
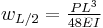 |
|
| Simply supported beam with asymmetric load | ||
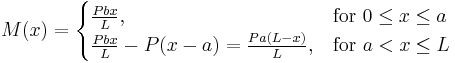 |
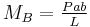 |
|
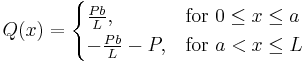 |
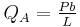
|
|
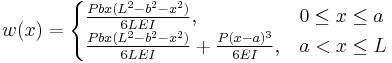 |
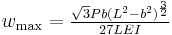
at |
|
Cantilever beams
Another important class of problems involves cantilever beams. The bending moments ( ) , shear forces (
) , shear forces ( ), and deflections (
), and deflections ( ) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below.[6]
) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below.[6]
| Distribution | Max. value | |
|---|---|---|
| Cantilever beam with end load | ||
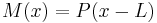 |
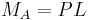 |
|
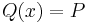 |
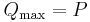 |
|
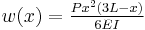 |
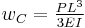 |
|
| Cantilever beam with uniformly distributed load | ||
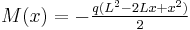 |
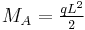 |
|
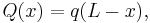 |
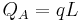 |
|
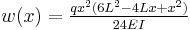 |
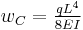 |
|
Solutions for several other commonly encountered configurations are readily available in textbooks on mechanics of materials and engineering handbooks.
Statically indeterminate beams
The bending moments and shear forces in Euler-Bernoulli beams can often be determined directly using static balance of forces and moments. However, for certain boundary conditions, the number of reactions can exceed the number of independent equilibrium equations.[6] Such beams are called statically indeterminate.
The built-in beams shown in the figure below are statically indeterminate. To determine the stresses and deflections of such beams, the most direct method is to solve the Euler–Bernoulli beam equation with appropriate boundary conditions. But direct analytical solutions of the beam equation are possible only for the simplest cases. Therefore, additional techniques such as linear superposition are often used to solve statically indeterminate beam problems.
The superposition method involves adding the solutions of a number of statically determinate problems which are chosen such that the boundary conditions for the sum of the individual problems add up to those of the original problem.
(a) Uniformly distributed load q. |
(b) Linearly distributed load with maximum q0 |
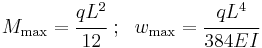 |
|
(c) Concentrated load P |
(d) Moment M0 |
Another commonly encountered statically indeterminate beam problem is the cantilevered beam with the free end supported on a roller.[6] The bending moments, shear forces, and deflections of such a beam are listed below.
| Distribution | Max. value | |
|---|---|---|
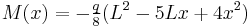 |
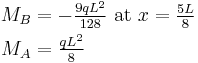 |
|
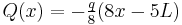 |
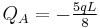 |
|
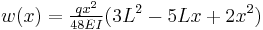 |
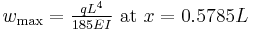 |
Extensions
The kinematic assumptions upon which the Euler-Bernoulli beam theory is founded allow it to be extended to more advanced analysis. Simple superposition allows for three-dimensional transverse loading. Using alternative constitutive equations can allow for viscoelastic or plastic beam deformation. Euler-Bernoulli beam theory can also be extended to the analysis of curved beams, beam buckling, composite beams, and geometrically nonlinear beam deflection.
Euler-Bernoulli beam theory does not account for the effects of transverse shear strain. As a result it underpredicts deflections and overpredicts natural frequencies. For thin beams (beam length to thickness ratios of the order 20 or more) these effects are of minor importance. For thick beams, however, these effects can be significant. More advanced beam theories such as the Timoshenko beam theory (developed by the Russian-born scientist Stephen Timoshenko) have been developed to account for these effects.
Large deflections
The original Euler-Bernoulli theory is valid only for infinitesimal strains and small rotations. The theory can be extended in a straightforward manner to problems involving moderately large rotations provided that the strain remains small by using the von Kármán strains.[7]
The Euler-Bernoulli hypotheses that plane sections remain plane and normal to the axis of the beam lead to displacements of the form
Using the definition of the Lagrangian Green strain from finite strain theory, we can find the von Karman strains for the beam that are valid for large rotations but small strains. These strains have the form
From the principle of virtual work, the balance of forces and moments in the beams gives us the equilibrium equations
where  is the axial load,
is the axial load, 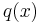 is the transverse load, and
is the transverse load, and
To close the system of equations we need the constitutive equations that relate stresses to strains (and hence stresses to displacements). For large rotations and small strains these relations are
where
The quantity 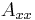 is the extensional stiffness,
is the extensional stiffness,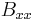 is the coupled extensional-bending stiffness, and
is the coupled extensional-bending stiffness, and 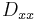 is the bending stiffness.
is the bending stiffness.
For the situation where the beam has a uniform cross-section and no axial load, the governing equation for a large-rotation Euler-Bernoulli beam is
See also
- Applied mechanics
- Bending
- Buckling
- Flexural rigidity
- Plate theory
- Sandwich theory
- Singularity function
- Strain (materials science)
- Theorem of three moments (Clapeyron's theorem)
- Three point flexural test
Notes
- ^ Timoshenko, S., (1953), History of strength of materials, McGraw-Hill New York
- ^ Truesdell, C., (1960), The rational mechanics of flexible or elastic bodies 1638-1788, Venditioni Exponunt Orell Fussli Turici.
- ^ Ballarini, Roberto (April 18, 2003). "The Da Vinci-Euler-Bernoulli Beam Theory?". Mechanical Engineering Magazine Online. http://www.memagazine.org/contents/current/webonly/webex418.html. Retrieved 2006-07-22.
- ^ Seon M. Han, Haym Benaroya and Timothy Wei (March 22, 1999) (PDF). Dynamics of Transversely Vibrating Beams using four Engineering Theories. final version. Academic Press. http://csxe.rutgers.edu/research/vibration/51.pdf. Retrieved 2007-04-15.
- ^ McKenzie, William (2006). Examples in Structural Analysis. Taylor & Francis.
- ^ a b c d e f g h Gere, J. M. and Timoshenko, S. P., 1997, Mechanics of Materials, PWS Publishing Company.
- ^ Reddy, J. N., (2007), Nonlinear finite element analysis, Oxford University Press.
References
- E.A. Witmer (1991-1992). "Elementary Bernoulli-Euler Beam Theory". MIT Unified Engineering Course Notes. pp. 5–114 to 5–164.
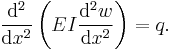
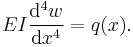
![S = \int_0^L \left[ \frac{1}{2} \mu \left( \frac{\partial w}{\partial t} \right)^2 - \frac{1}{2} EI \left( \frac{ \partial^2 w}{\partial x^2} \right)^2 %2B q(x) w(x,t)\right] dx](/2012-wikipedia_en_all_nopic_01_2012/I/e87dd17b2db93ecf2d104289106f1b03.png)
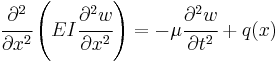
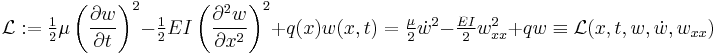
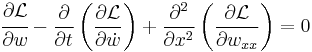
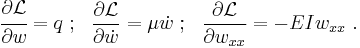
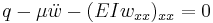
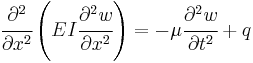
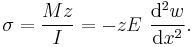
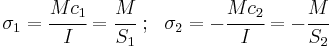
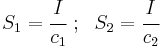
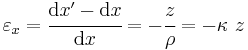
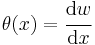
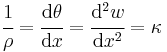
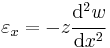
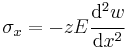
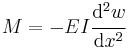
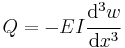
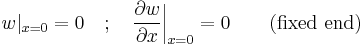
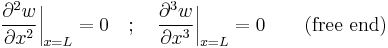
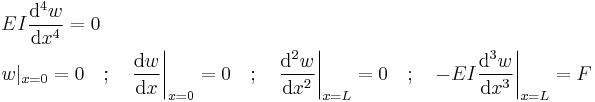
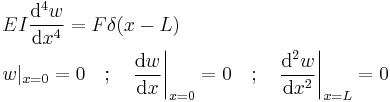
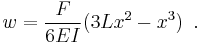
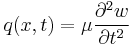
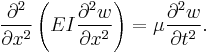
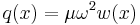
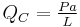
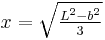
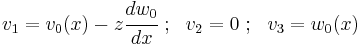
![\begin{align}
\varepsilon_{11} & = \cfrac{du_0}{dx_1} - x_3\cfrac{d^2w_0}{dx_1^2} %2B
\frac{1}{2}\left[
\left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right)^2 %2B
\left(\cfrac{dw_0}{dx_1}\right)^2\right] \\
\varepsilon_{22} & = 0 \\
\varepsilon_{33} & = \frac{1}{2}\left(\cfrac{dw_0}{dx_1}\right)^2 \\
\varepsilon_{23} & = 0 \\
\varepsilon_{31} & =
\frac{1}{2}\left(\cfrac{dw_0}{dx_1}-\cfrac{dw_0}{dx_1}\right) -
\frac{1}{2}\left[\left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right)
\left(\cfrac{dw_0}{dx_1}\right)\right] \\
\varepsilon_{12} & = 0
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/a9bef33f65804141cd764b705d66a7e3.png)
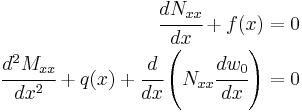
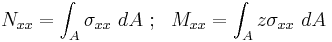
![\begin{align}
N_{xx} & =
A_{xx}\left[\cfrac{du_0}{dx} %2B \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] -
B_{xx}\cfrac{d^2w_0}{dx^2} \\
M_{xx} & =
B_{xx}\left[\cfrac{du_0}{dx} %2B \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] -
D_{xx}\cfrac{d^2w_0}{dx^2}
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/10eeeb97b8f5ffebe90a8a8f59506536.png)